【题解】会场安排问题

题目链接：会场安排问题

题意：

有n个活动，给定每个活动的开始和结束时间区间[l,r)，同时间一个会场内只能容纳一个活动，问最少需要多少会场。

思路：

• 很容易想到贪心，按照结束时间排序然后遍历活动为每个会场找到可容纳最多活动。但是这样做是不对的，我们可以看这四个活动：
  
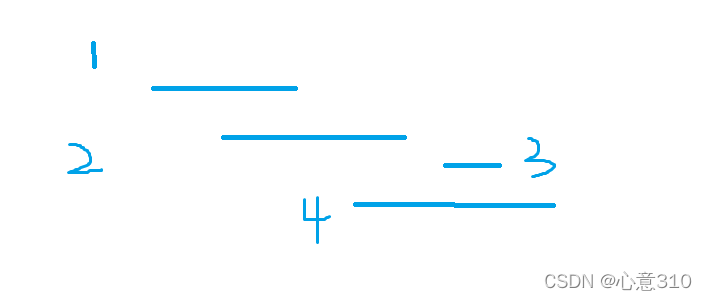
• 通过目测我们很容易看到，1和4，2和3可以安排在一个会场，共计只需要2个会场的场地。
• 但是当我们按照结束时间排序后会发现，我们遍历数组会将1和3安排在一起，而2和4时间冲突，我们不得不为4个活动安排3个场地。
• 1.为什么会产生这样的问题？2. 该怎样解决？1.为了最少的安排场地，我们是希望各个活动之间紧凑一点，最好是一个活动刚刚结束另一个活动就开始。为了达到这个目的我们并不关心结束时间会不会很晚。这显然与贪心香悖。2.我们可以按照开始时间排序，通过优先队列每次看最早结束的那个场地是否能接纳最新的活动。

PS:

网上还有个神乎其技的写法，将开始时间和结束时间分别排序，然后用两个指针分别指向开始时间和结束时间。如果当前开始时间小于当前结束时间，ans++，否则让结束时间向后移动一位。最后ans就是结果，将双指针算法和贪心结合在一起，叹服叹服~。

错误示范：

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
#include<queue>
#include<set>
#include<map>

using namespace std;
const int N = 10010,INF=0x3f3f3f3f;
typedef pair<int, int> PII;
typedef long long ll;

int n,v[N];
PII p[N];//first结束时间  second开始时间
int main()
{
	cin >> n;
	for (int i = 0; i < n; ++i)cin >> p[i].second >> p[i].first;

	sort(p, p + n);

	int res=0;
	while (1)
	{
		int end = 0;
		
		for (int i = 0; i < n; ++i)
		{
			if (end < =p[i].second && !v[i])
			{
				end = p[i].first;
				v[i] = 1;
			}
		}

		if (end) res++;
		else break;
	}

	cout << res << endl;

	return 0;
}

AC代码：

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
#include<queue>
#include<set>
#include<map>

using namespace std;
const int N = 10010, INF = 0x3f3f3f3f;
typedef pair<int, int> PII;
typedef long long ll;

int n, v[N];
vector<PII>p;//first开始时间 second结束时间
priority_queue<PII, vector<PII>, greater<PII>>q;

int main()
{
	cin >> n;
	for (int i = 0; i < n; ++i)
	{
		PII a; 
		//注意，求最少活动场数不能用结束时间来排序，否则将会出现同场地不同活动之间大量空隙的现象
		cin >> a.first >> a.second ;
		p.push_back(a);
	}

	sort(p.begin(), p.end());

	int res=n;
	q.push({ p[0].second,p[0].first });
	for (int i = 1; i < n; ++i)
	{
		PII a = q.top();
		if (p[i].first >= a.first)
		{
			q.pop();
			res--;
		}
		q.push({ p[i].second,p[i].first});
	}

	cout << res;

	return 0;
}