【题解】区间覆盖

题目：区间覆盖

题意：

给定 N 个闭区间 [ai,bi] 以及一个线段区间 [s,t]，请你选择尽量少的区间，将指定线段区间完全覆盖。

输出最少区间数，如果无法完全覆盖则输出 −1。

输入格式

第一行包含两个整数 s 和 t，表示给定线段区间的两个端点。

第二行包含整数 N，表示给定区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式

输出一个整数，表示所需最少区间数。

如果无解，则输出 −1。

数据范围

1 ≤ N ≤ 10⁵,
−10⁹ ≤ ai ≤ bi ≤ 10⁹,
−10⁹ ≤ s ≤ t ≤ 10⁹

输入样例：

1 5
3
-1 3
2 4
3 5

输出样例：

2

思路：

• 第一步：将所有区间按左端点排序。
• 第二步：依次枚举每个区间，在所有能覆盖 start 的区间中，选择右端点最大的区间，然后更新 start 为右端点的最大值。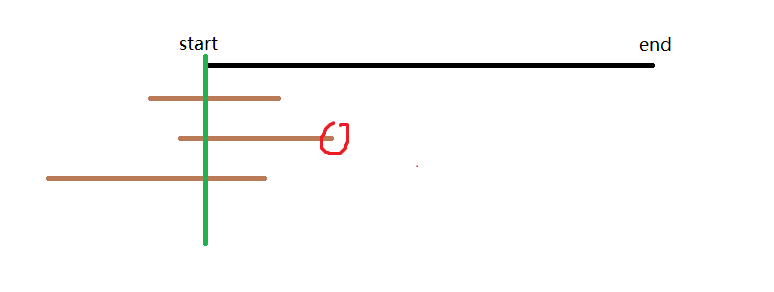
• 

代码

特判第一个区间，更容易理解

#include<iostream>
#include<algorithm>

using namespace std;

const int N=100010;
#define PII pair<int,int>

int n,st,ed;
PII p[N];

int main()
{
    cin>>st>>ed>>n;
    for(int i=1;i<=n;++i)cin>>p[i].first>>p[i].second;
	//排序
    sort(p+1,p+n+1);
    
    int res=0,max_r;
    //特判第一个区间，如果第一个区间都不能覆盖start，说明无法将给定区间全部覆盖
    if(p[1].first>st)
    {
        cout<<-1;
        return 0;
    }
    else 
    {
        res++;
        max_r=p[1].second;
    }
    for(int i=2;i<=n;++i)
    {
        //已经全部覆盖
        if(max_r>=ed)break;
        //能够覆盖start，更新max_r
        if(p[i].first<=st)
            max_r=max(max_r,p[i].second);
        //不能覆盖start，那么记录新的start，并更新max_r
        if(p[i].first>st && p[i].first<=max_r && p[i].second>max_r)
        {
            res++;
            st=max_r;
            max_r=p[i].second;
        }
    }
    //如果更新完后依然无法覆盖给定区间的右端点，那么输出-1
    (max_r<ed)?cout<<-1:cout<<res;
    return 0;
}

不特判第一个区间，代码更优雅

#include<iostream>
#include<algorithm>

using namespace std;

const int N=100010;
#define PII pair<int,int>

int n,st,ed;
PII p[N];

int main()
{
    cin>>st>>ed>>n;
    for(int i=1;i<=n;++i)cin>>p[i].first>>p[i].second;

    sort(p+1,p+n+1);
    
    int res=0,max_r=st,st=-0x3f3f3f3f;
    
    for(int i=1;i<=n;++i)
    {
        if(p[i].first<=st)
            max_r=max(max_r,p[i].second);
    	//注意，p[i].second>=max_r这里比较难理解，可以在纸上画一下帮助理解
        //或者在这个if前后输出st,ed,p[i].first,p[i].second看一下更为直观
        if(p[i].first>st && p[i].first<=max_r && p[i].second>=max_r)
        {
            res++;
            st=max_r;
            max_r=p[i].second;
        }
    
        //当覆盖区间的最大右端点已经能够覆盖给定区间的右端点时退出
        if(max_r>=ed)break;
    }
    //如果res为0或者无法覆盖整个区间，输出-1
    (!res||max_r<ed)?cout<<-1:cout<<res;
    return 0;
}