【模板】归并排序

归并排序代码模板

void merge_sort(int l, int r)
{
    if(l >= r)return ;

    int mid = (l + r)>>1;
    merge_sort(l, mid),merge_sort(mid + 1, r);
    
    int k = 0, i = l, j = mid + 1;
    while(i <= mid&&j <= r)
    {
        if(a[i] < a[j])temp[k ++] = a[i ++];
        else temp[k ++] = a[j ++]; //要求逆序对的话，在else的作用域中额外加 ans+=(mid-i+1)
    }
    while(i <= mid) temp[k ++] = a[i ++];
    while(j <= r) temp[k ++] = a[j ++];
    
    for(i = l, j = 0; i <= r; ++ i, ++ j)a[i] = temp[j];
}

归并图示步骤：

1. 确定分界点：数列中点， mid=(l+r)/2 。
2. 归并排序左半边和右半边。
3. 将排序好的左右两边归并，合二为一。

归并细节

• 确定递归终结条件 l>=r 。
• 分别递归左右两边。
• 将排序好的两边合二为一，排序实际上就隐含在合并的过程中了。
• 合并排序是稳定O(n*log(n))的复杂度，而且是稳定的，但是相对于快排需要额外开辟一个数组。
• 归并排序的思想 - 基于分治。

题目：归并排序

题意：

给定你一个长度为 n 的整数数列。

请你使用归并排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式

输入共两行，第一行包含整数 n。

第二行包含 n 个整数（所有整数均在 1∼10⁹ 范围内），表示整个数列。

输出格式

输出共一行，包含 n 个整数，表示排好序的数列。

数据范围

1 ≤ n ≤ 100000

输入样例：

5
3 1 2 4 5

输出样例：

1 2 3 4 5

排序代码

#include<iostream>

using namespace std;

const int N = 1e5 + 5;

int a[N],temp[N];

void merge_sort(int l, int r)
{
    if(l >= r)return ;

    int mid = (l + r)>>1;//中点
    merge_sort(l, mid),merge_sort(mid + 1, r);//递归左右两半边
    
    int k = 0, i = l, j = mid + 1;//i和j分别作为左右两边的起点
    while(i <= mid&&j <= r)
    {//两边都还有剩余
        if(a[i] < a[j])temp[k ++] = a[i ++];
        else temp[k ++] = a[j ++];
    }
    while(i <= mid) temp[k ++] = a[i ++];//左半边有剩余
    while(j <= r) temp[k ++] = a[j ++];//右半边有剩余
    
    for(i = l, j = 0; i <= r; ++ i, ++ j)a[i] = temp[j];//合并好后返回给原数组
}

int main()
{
    int n;
    scanf("%d", &n);
    for(int i = 0; i < n; ++ i) scanf("%d", &a[i]);
    
    merge_sort(0, n-1);
    
    for(int i = 0; i < n; ++ i) printf("%d ", a[i]);
    
    return 0;
}

利用归并排序寻找给定数列的逆序对的数量

题目：逆序对的数量

题意：

给定一个长度为 n 的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i<j 且 a[i]>a[j]，则其为一个逆序对；否则不是。

输入格式

第一行包含整数 n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式

输出一个整数，表示逆序对的个数。

数据范围

1 ≤ n ≤ 100000，
数列中的元素的取值范围 [1, 10⁹]。

输入样例：

6
2 3 4 5 6 1

输出样例：

5

思路：

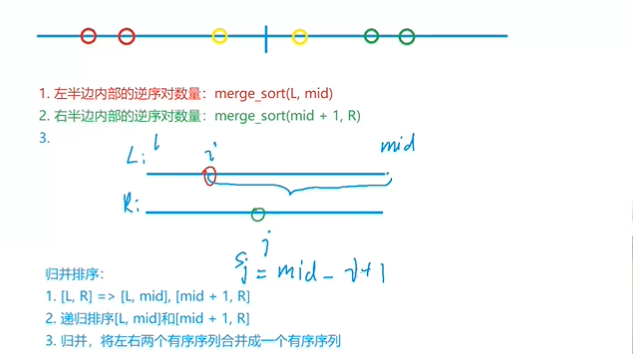
• 根据上图我们可以发现，实际上所有的逆序对可以分为三种情况，我们重点分析第三种情况（后面会说原因）
• 分别在左右两侧的逆序对数量实际上在归并的过程中就可以得到，因为左右两侧都是有序数列
• 那么怎么去得到左边和右边的逆序对数量呢，我们会发现如果只看左边，问题回到了开始：求给定数列的逆序对
• 所以我们在不断向下递归的过程中就已经将情况1和情况2解决
• 注意：两个数字如果大小相同则不属于逆序对

逆序对代码

#include<iostream>

using namespace std;

const int N= 1e5+5;

int a[N],temp[N];
long long ans=0;

void merge_sort(int l,int r)
{
    if(l>=r)return ;
    
    int mid=(l+r)>>1;
    merge_sort(l,mid),merge_sort(mid+1,r);
    
    int k=0,i=l,j=mid+1;
    while(i<=mid&&j<=r)
    {
        //务必注意，两个数字相同时不属于逆序对，必须严格符合前大后小
        if(a[i]<=a[j])temp[k++]=a[i++];//条件必须是a[i] <= a[j]
        //如果数列1中第i个数大于数列2中第j个数，那么数列1中i之后的所有均大于j，那么就会产生(mid-i+1)个逆序对
        else temp[k++]=a[j++],ans+=(mid-i+1);
    }
    while(i<=mid)temp[k++]=a[i++];
    while(j<=r)temp[k++]=a[j++];
    
    for(i=l,j=0;i<=r;i++,j++)a[i]=temp[j];
}
int main()
{
    int n;
    scanf("%d",&n);
    
    for(int i=0;i<=n;++i)scanf("%d",&a[i]);
    
    merge_sort(0, n-1);
    
    printf("%lld",ans);
    return 0;
}