算法分析与设计-算法实验（一）

前言

尝试用最朴素的语言，将问题阐释清楚。

算法实验1：4800 x^n mod 1003

题目： x^n mod 1003

题意：

给定整数x和n,求x的n次幂 mod 1003

输入格式

整数x和n。

输出格式

xⁿ mod 1003

数据范围

1<=x,n<=1,000,000,0000

输入样例：

2 10

输出样例：

21 

思路：

• 递归用 快速幂思想。考虑如何快速计算 x^n ，将x反复乘 n-1 个x吗？如果n的级别达到1e9的复杂度，运行时间将会很慢。如何优化？我们注意到当n为偶数时， x^n = (x^2)^(n/2) ；当n为奇数时，因为整数除法向下取证，所以我们在进行 n/2 操作时损失了一个底数（例如当n=7时，n/2=3，x²3=x^6），所以需要额外乘一个当前底数（为什么不说x，而是用底数这个词？因为在递归的过程中底数需要平方，所以是一直在变的，我们每次单独乘底数的时候是乘当前的底数）。
• 这时我们会发现，每将x平方一次，n的值就会减少一半，这显然大大提高了运行速度。
• 二进制做法 。首先需要认同一个公式：x^n=x^M ，M为n的二进制。这其实很好理解，M的二进制依然等于n，x的相同幂次一定相同。求x^M就会简单很多，M可以分解为许多二进制相加，也即x^(m1+m2+...+mp)，直观来看m1 ~ mp其实1 2 4 8 … 中的某些数，这些数代表了M二进制中1的位置所代表的数，例如n=10，则M=1010，那么m1=2，m2=8，均转为二进制m1=10，m2=1000，x^(m1+m2+...+mp)=(x^m1)*(x^m2)*(x^m3)... （请务必反复体会该方程，这是理解后续操作的关键），所有的m均是2的某个次方且均不相同，结合递归做法的思想中我们会发现，将底数x平方某些次数后，可以将m转为1（也即通过改变底数，将幂改为1，而结果不变），那么要将x平方几次呢？只要平方m二进制的位数次即可（每平方一次，m的值缩小一倍，m最低位记为0）。
• 那么我们就会发现，其实我们只要从低位开始遍历M，将底数不断平方，在M当前位数是1时，乘一次当前的底数，最后的计算结果就是我们所要求的结果——x^M。

递归代码：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<bits/stdc++.h>
 
using namespace std;
 
#define ll long long
const ll M=1003;
 
//返回x^k
ll slove(ll x,ll k,ll res)
{
    if(k<=0)return res;//幂等于0，结束递归
    if(k%2==1) //幂为奇数，额外乘一次当前底数
        res=res*x%M;
    x=x*x%M;//底数平方
    k/=2;//幂减小一半
    return slove(x,k,res);//继续递归，直到幂为0
}
 
int main()
{
    ll n,k;
    cin>>n>>k;
    n%=M;
    ll ans=slove(n,k,1);
    cout<<ans;
    //system("pause");
    return 0;
}

二进制代码：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<bits/stdc++.h>
 
using namespace std;
 
#define ll long long
const int M=1003,N=1e5+10;
bool a[N];//从低位开始存二进制
 
int main()
{
    ll n,k;
    cin>>n>>k;
    n%=M;
    if(k==1)
    {
        cout<<n%M;
        return 0;
    }
 
    ll m=0,u=k;
    while(u)
    {
        a[m++]=u&1;
        u/=2;
    }
 
    ll sum=1;
    for(ll i=0;i<m;++i)
    {
        if(a[i])sum=sum*n%M;
        n=n*n%M;
    }
    cout<<(sum+M)%M<<endl;
    //system("pause");
    return 0;
}

算法实验二：4801 汉诺塔

题目：汉诺塔

题意：

汉诺塔（又称河内塔）问题是印度的一个古老的传说。开天辟地的神勃拉玛在一个庙里留下了三根金刚石的棒A、B和C，A上面套着n个圆的金片，最大的一个在底下，其余一个比一个小，依次叠上去，庙里的众僧不倦地把它们一个个地从A棒搬到C棒上，规定可利用中间的一根B棒作为帮助，但每次只能搬一个，而且大的不能放在小的上面。僧侣们搬得汗流满面，可惜当n很大时这辈子恐怕就很搬了 聪明的你还有计算机帮你完成，你能写一个程序帮助僧侣们完成这辈子的夙愿吗？

输入格式

输入金片的个数n。这里的n<=10。

输出格式

输出搬动金片的全过程。格式见样例。

数据范围

n<=10

输入样例：

2

输出样例：

Move disk 1 from A to B
Move disk 2 from A to C
Move disk 1 from B to C

思路：

• 我的拙见：对于递归要从思想着手去理解，因为递归的本质是分解问题。将一个大问题不断细分，找到问题的共同点，从而在解决小问题的过程中逐步解决大问题。
• 例如该题中，要求我们将n块石板借助B石柱，从A石柱移动到C石柱。n块石板不好解决，那么一块石板呢？我们可以立即发现可以直接从A移动到C。如果是两块石板呢？我们可以先将一块放到B上，然后将A剩下的一块石板移动到C上，然后将B上的石板移动到C上。那么三块石板呢？我们需要先将上面两块石板移动到B上，然后才能将A最后一块石板移动到C上。怎么移动呢？我们可以借助C。先将第一块石板放到C上，再将第二块石板放到B上，然后把第一块石板从C移动到B，然后将第三块石板移动到C，剩下的操作就是将B上的两块石板借助A移动到C了。
• 四块呢？我们会发现其实和三块时的解决方法是一样的，先将n-1块从A移动到B上，将最后一块从A移动到C，然后将B上的n-1块石板借助A移动到C。怎么实现？事实上我们将上述过程写出来，发现只有区区4行关键代码，不得不感慨实在是amazing~
• 思路参考：汉诺塔题解 | ❤梧桐苑 （其实也是我写的hhh）

代码：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<bits/stdc++.h>
 
using namespace std;
 
#define ll long long
const int M=1003,N=1e5+10;
bool a[N];//从低位开始存二进制
 
void slove(int n,char a,char b,char c)
{
    if (n == 1)cout <<"Move disk "<<1<<" from " << a << " to " << c << endl;
    else
    {
        slove(n - 1, a, c, b);
        cout << "Move disk " << n << " from " << a << " to " << c << endl;
        slove(n - 1, b, a, c);
    }
}
int main()
{
    int n;
    cin >> n;
    slove(n,'A','B','C');
    //system("pause");
    return 0;
}

算法实验3：4002 骨牌铺方格

题目： 骨牌铺方格

题意：

在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数. 例如n=3时,为2× 3方格，骨牌的铺放方案有三种,如下图：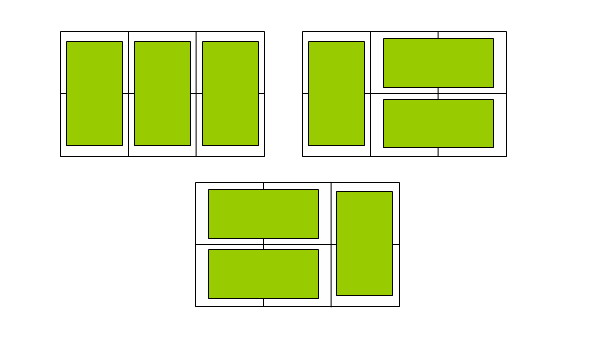

输入格式

输入数据由多行组成，每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0< n<=50)。

输出格式

对于每个测试实例，请输出铺放方案的总数，每个实例的输出占一行。

数据范围

2×n (0< n<=50)

输入样例：

1
3
2

输出样例：

1
3
2

思路：

• 本题需要用到 long long 数据类型。

• 本题可以用递归和矩阵快速幂两种方法实现。

• 递归。首先我们会发现，当方格的宽度是1时，只有一种方法实现。当方格宽度是2时，只有两种方法实现。当方格宽度是3时呢？问题开始变得有趣。首先我们已经确定，我们已经得到宽度分别为1和2的方格所有的组成方式 （这是解决问题的关键）。我们可以通过观察发现：如果我们在宽度为1的方格后加上两个叠着横放的方格，那么就可以组成宽度为3的方格；而在宽度为2的方格后放一个竖着的方格，也可以组成宽度为3的方格。有人可能会问，为什么不在宽度为1的方格后加两个竖着的方格组成宽度为3的方格呢？这是因为如果这样就会和宽度为2的方格重复（当我们放上第一个竖着的方格，我们得到宽度为2的方格，而我们已经保证宽度为2的当我们放上第二个竖着的方格，我们重复了之前对宽度为2的方格所进行的操作）。我们已经保证组成1和2的所有组成方式都找到了且均不相同，然后又在后面加入了不同的方格（对于宽度为1的方格，我们加入了两个叠着横放的；对于宽度为2的方格，我们加入了一个竖着的），那么就可以保证这些宽度为3的方格均不相同，且这就是所有的组成方式。

• 于是我们得到递推关系：
  $$
  F(n)=F(n-1)+F(n-2)
  $$

• 根据上式我们很容易就可以写出递归函数，但是需要注意的是我们需要提前用一个数组记录中间算过的某些值，例如用a[n]记录F(n)的值，因为当我们算F(n-1)时需要用F(n-2)和F(n-3)，而如果在计算F(n)时，又要重新计算F(n-2)的话，时间复杂度将大大升高，所以如果提前记录已经递归过的某些值，将节约很多运行时间。

• 矩阵快速幂。我们已经知道了第n项的值是前两项值的和，怎么在只知道第一项和第二项值的前提下，得到第n项的值呢？难道只能通过斐波那契的方式来做吗？我们可以换个思路，如果有某种运算，可以使得(a,b)（a是第一项，b是第二项）在经过运算后得到(b,a+b)，那么运算n-1次一样可以得到第n项的值。这种神奇的运算就是矩阵相乘。一个2×2的01矩阵可以帮助我们完成这样的运算。那么问题就就变为了怎么快速完成n-1次矩阵相乘的运算。运算n-1次吗？时间复杂度会很高，这个时候其实我们又回到了快速幂的思路上，通过改变底数（矩阵本身的值），就可以快速的降低幂的级别。这就是所谓的矩阵快速幂，矩阵只是运算的一种直观体现形式，其核心思想仍然是快速幂。

• 为什么初始01矩阵长这样？为什么矩阵相乘也能用快速幂？答案：易得、显然、略。

• (矩阵的本质是什么？ - 知乎 (zhihu.com)

递归代码：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<bits/stdc++.h>
 
using namespace std;
 
#define ll long long
const int M=1003,N=1e5+10;
ll a[N];//从低位开始存二进制
 
ll slove(ll n)
{
    if(a[n])return a[n];
    if(n<=2)
    {
        a[n]=n;
        return n;
    }
    a[n]=slove(n-1)+slove(n-2);
    return a[n];
}
 
int main()
{
    ll n;
    while(cin>>n)
    {
        ll res=slove(n);
        cout<<res<<endl;        
    }
    //system("pause");
    return 0;
}

矩阵快速幂代码

#include<iostream>
#include<algorithm>
#include<cmath>
#include<bits/stdc++.h>
 
using namespace std;
 
#define ll long long
const int M=1003,N=1e5+10;
//        [1,1]
//[a,b] * [1,0] = [a+b,a]
 
//                [1,1]
//可得  [1,1] * ( [1,0] )^n = [F(n+1),F(n)]
 
// a1,a2
// b1,b2
class matrix
{                        
    public:
        ll a1=1,a2=1,b1=1,b2=0;
        matrix operator*(const matrix a)
        {
            matrix b;
            b.a1=a1*a.a1+a2*a.b1;
            b.a2=a1*a.a2+a2*a.b2;
            b.b1=b1*a.a1+b2*a.b1;
            b.b2=b1*a.a2+b2*a.b2;
            return b;
        }
};
int main()
{
    ll n;
    while(cin>>n)
    {
        n--;//初始的时候就是第一项，乘完第一个矩阵得到第二项
        matrix x,k;
        while(n>0)
        {
            if(n&1)x=x*k;
            n/=2;
            k=k*k;
        }
        //cout<<x.a1<<" "<<x.a2<<" "<<x.b1<<" "<<x.b2<<endl;
        cout<<x.a1<<endl;
    }
    //system("pause");
    return 0;
}

算法实验4：4003 棋盘覆盖

题目： 棋盘覆盖

题意：

在一个2^k x 2^k 个方格组成的棋盘中，恰有一个方格与其他方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。

输入格式

k，dr，dc。k定义如前，dr，dc分别表示特殊方格所在的行号和列号 1= < k < =6

输出格式

按照左上，右上，左下，右下的顺序用分治法求解。特殊方格标0，其他位置按上述顺序依次标记。

数据范围

1= < k < =6

输入样例：

2 1 1

输出样例：

2 2 3 3 
2 0 1 3 
4 1 1 5 
4 4 5 5  

思路：

• 分治 。什么是分治？比如我们有10个苹果，要我们找出最重的一个，怎么找？我们会两个两个比较，轻的排除，重的留下。最后剩下的那个就是最重的对吧，其实这就已经涉及到了分治的思想。所谓分治，就是把大的问题分解，只要我们无法立即解决该问题就接着分解，直到我们可以直接解决所分解出来的子问题时，我们就停止分解并解决子问题。通过解决子问题最终解决大问题。比如我们无法直接得到10个苹果中谁是最重的一个，但是我们可以知道两个苹果中谁更重，那我们就两个两个比，这样比下去就可以得到10个里谁最重。分治就是这样。
• 怎么利用分治解决该问题？还是像苹果那样思考，一个10×10有特殊方格的棋盘我们很难直接覆盖，那么一个2×2有特殊方格的棋盘呢？我们可以立即解决，直接在另外三个正常方格上放骨牌就好了嘛。考虑4×4的棋盘呢？我们分成4个2×2有特殊方格的棋盘就好了呀，怎么分呢？由于骨牌占三个方格，而特殊方格一定在所分的四个小棋盘中某个，所以我们直接将三个自定义的特殊方格放在最中间（也即四个小棋盘的两个分界线的交汇处），使其能够组成一个骨牌状就好了。8×8呢？我们发现还是和4×4一样的做法，只要我们解决不了当前的问题，那就将问题分解，直到我们可以解决。
• 为什么要分成四个有特殊方格的棋盘？因为整个大问题就是有特殊方格的，为了保持问题的一致性， 我们所分解的小方格也要有特殊方格，只不过我们自定义的特殊方格可以放骨牌。
• 怎么确定特殊方格的位置？因为我们分解成了四个小棋盘，原特殊方格一定在四个小棋盘之一，所以我们需要将另外三个自定义的特殊方格放在一起，可以用一个骨牌将三个自定义特殊方格全部覆盖就好了，放在哪呢？显然我们要放在整个大棋盘的最中央。具体特殊方格在小棋盘中的位置，要根据小棋盘在大棋盘中的位置来确定。

递归代码：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<bits/stdc++.h>
 
using namespace std;
 
#define ll long long
const int M=1003,N=1e2+50;
 
int m[N][N],Case;
 
//将整个大矩阵不断分解为4个均含有特殊格的小矩阵，以此将问题规模缩小。
//根据小矩阵的位置设置特殊方格位置
void chessBoard(int sz,int dr,int dc,int lr,int lc)//2^k (dr,dc)特殊格位置 (lr,lc)分治左上角位置
{
    if(sz==1)return ;
    int t=++Case,s=sz/2;
 
    if(dr<lr+s&&dc<lc+s) chessBoard(s,dr,dc,lr,lc);//1  左上
    else
    {
        m[lr+s-1][lc+s-1]=t;//左上矩阵特殊方格的位置在自己的右下
        chessBoard(s,lr+s-1,lc+s-1,lr,lc);
    }
 
    if (dr<lr+s&&dc>=lc+s) chessBoard(s,dr,dc,lr,lc+s);//2  右上
    else    
    {
        m[lr+s-1][lc+s]=t;//右上矩阵特殊方格的位置在自己的左下
        chessBoard(s,lr+s-1,lc+s,lr,lc+s);
    }
 
    if (dr>=lr+s&&dc<lc+s)chessBoard(s,dr,dc,lr+s,lc);//3  左下
    else
    {
        m[lr+s][lc+s-1]=t;//左下矩阵特殊方格的位置在自己的右上
        chessBoard(s,lr+s,lc+s-1,lr+s,lc);
    }
 
    if (dr>=lr+s&&dc>=lc+s)chessBoard(s,dr,dc,lr+s,lc+s);//4  右下
    else
    {
        m[lr+s][lc+s]=t;//右下矩阵特殊方格的位置在自己的左上
        chessBoard(s,lr+s,lc+s,lr+s,lc+s);
    }
}
 
int main()
{
    int k,dr,dc;
    cin>>k>>dr>>dc;
    k=pow(2,k);
    //cout<<k<<endl;
    chessBoard(k,dr,dc,0,0);
    for(int i=0;i<k;++i)
    {
        for(int j=0;j<k;++j)
            cout<<m[i][j]<<" ";
        cout<<endl;
    }
    //system("pause");
    return 0;
}

算法实验5：4004 求最大和最小值

题目： 求最大和最小值

题意：

包含多组测试数据。每组测试数据的第一个元素是整数的个数n,接下来是n个整数。0表示结束。 n<=200

输入格式

k，dr，dc。k定义如前，dr，dc分别表示特殊方格所在的行号和列号 1= < k < =6

输出格式

这n个数中的最大值和最小值。

数据范围

n<=200

输入样例：

5 1 8 2 4 3
3 2 4 1
0

输出样例：

8 1
4 1

思路：

• 循环分治 。1.每次成对从数列中取出两个数。2.比较两个数，将两个数中较大值记为a，较小值记为b。3.将a与 *max进行比较，如果a> *max，更新 *max的值。4.将b与 *min进行比较，如果b< *min，更新 *min的值。ps：为了防止最后只剩一个数无法取对，需要提前根据数列的奇偶特判一下

• 可以发现，我们共取出n/2对数，每对数共比较3次，所以时间复杂度为╔ 3n/2 ╕，而根据奇偶我们会提前取出1或2个数，如果为奇数
  时间复杂度为╔3(n-1)/2╕==╔3n/2-3/2╕，如果是偶数╔3(n-2)/2╕==╔3n/2-3╕

• 递归分治 。和循环差不多，还是不断细分到问题规模只有1个数或者2个数，比较出最大值和最小值后，通过自定义的m1，m2，n1，n2回溯。额外需要注意的是：maxmin(a,l,mid,&m1,&n1); maxmin(a,mid+1,r,&m2,&n2); 这两行代码执行完后，m1和n1中已经存好了整个数组前半部分的最大值和最小值，m2和n2存好了后半部分的最大值和最小值。后面的四句 if-else 则比较出了整个数组的最大值和最小值。

• 时间复杂度严格证明：

       { 1        n<=2}
  T(n)={ 2T(n/2)+2 n>2}
  
  T(n)=2T(n/2)+2;
  设n=2^k
  可以得到 T(n)=2T(n/2)+2
     		    =2(2T(n/4)+2)+2;
     		    =(2^2) * T(n/4)+2^2+2;
     			=2^(k-1) * T(2)+2^(k-1)+...+2;
     			=3 * 2(k-1)-2=3 * n/2-2

循环代码：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<bits/stdc++.h>
  
using namespace std;
  
#define ll long long
const int M=1003,N=1e2+50;
  
void maxmin(int a[],int low,int high,int *max,int *min)
{
    int n=high+1,k=0;
    if(n&1)
    {
        *max=*min=a[0];
        k++;
    }
    else
    {
        if(a[0]>a[1])
        {
            *max=a[0];
            *min=a[1];
        }
        else
        {
            *max=a[1];
            *min=a[0];
        }
        k+=2;
    }
    for(int i=k;i<n;i+=2)
    {
        if(a[i]>a[i+1])
        {
            if(a[i]>*max)*max=a[i];
            if(a[i+1]<*min)*min=a[i+1];
        }
        else
        {
            if(a[i+1]>*max)*max=a[i+1];
            if(a[i]<*min)*min=a[i];
        }
    }
}
int main()
{
    int max,min,k,a[200];
    int m;
    while(scanf("%d",&k)&&k)
    {
        for(m=0;m<k;m++)
            scanf("%d",&a[m]);
        maxmin(a,0,k-1,&max,&min);
        printf("%d %d\n",max,min);
    
    }
    
} 

递归代码：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<bits/stdc++.h>
  
using namespace std;
  
#define ll long long
const int M=1003,N=1e2+50;
  
void maxmin(int a[],int low,int high,int *max,int *min)
{
    int l=low,r=high,mid=l+r>>1;
    if(l==r)*max=*min=a[l];
    else if(r-l==1)
    {
        if(a[l]>a[r])
        {
            *max=a[l];
            *min=a[r];
        }
        else
        {
            *max=a[r];
            *min=a[l];
        }
    }
    else
    {
        int m1,m2,n1,n2;
        maxmin(a,l,mid,&m1,&n1);
        maxmin(a,mid+1,r,&m2,&n2);
        
        if(m1>m2) *max=m1;
        else *max=m2;
        if(n1<n2) *min=n1;
        else *min=n2;
    }
}
int main()
{
    int max,min,k,a[200];
    int m;
    while(scanf("%d",&k)&&k)
    {
        for(m=0;m<k;m++)
            scanf("%d",&a[m]);
        maxmin(a,0,k-1,&max,&min);
        printf("%d %d\n",max,min);
    
    }
    
}