写在前面
很诚恳的说,本文 并非详实 (这可能意味着需要读者亲自思考)的“答案”,仅为笔者在复习题目(预习)时的体会和心得,当然也会给出对笔者有帮助的资料以供读者参阅。随着考试临近,本文将随着笔者再次复习题目而同步更新,解析或将更加细腻,若有问题可在评论区留言,下一次更新将修改相关描述。
另外,本文需要配合老师所给出的 PTT 作为资料(如果你已经有了一定基础,也可以只看本文,因为相应题目笔者已经给出)。下面是 PPT 下载链接:
第二章
前缀知识
DFA(Deterministic Finite Automaton)和 NFA(Nondeterministic Finite Automaton)都是有限自动机模型,用于描述和识别形式语言。
DFA 是一种确定性有限自动机,它在给定输入字符和当前状态的情况下,根据提前定义好的状态转移函数,唯一地确定下一个状态。换句话说,从每个状态出发,对于给定的输入字符,只能到达一个特定的下一个状态。DFA 拥有确定性,因为它的状态转移是确定的。
NFA 是一种非确定性有限自动机,相比于 DFA,它在给定输入字符和当前状态的情况下,可以有多个可能的下一个状态。这意味着在某个状态下,对于给定的输入字符,可以选择多个转移路径。NFA 的状态转移是非确定的,因此它可以同时处于多个状态。
2.3 题
题目 :叙述由下列正规式描述的语言
解析 :找没有闭包符号 * 的字符,描述这些字符的 个数 和 数量 。
2.7 题
题目 :用算法 2.4 为下列正规式构造 NFA,并给出处理 ababbab 的状态转换序列
解析 :
注意基本符号 NFA 的构造,比如想要推导出 (a|b) 那么就需要画出如下的图:
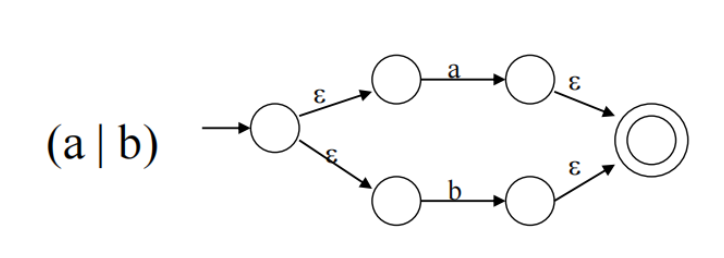
以小见大,就很容易理解 (a|b)*a 的构造了,因为 * (闭包)表示可以选任意次,当选 0 次时就需要有一条线从结点 0 指向 7,当选任意次时需要有一条从 6 指向 1 的线。如下所示:
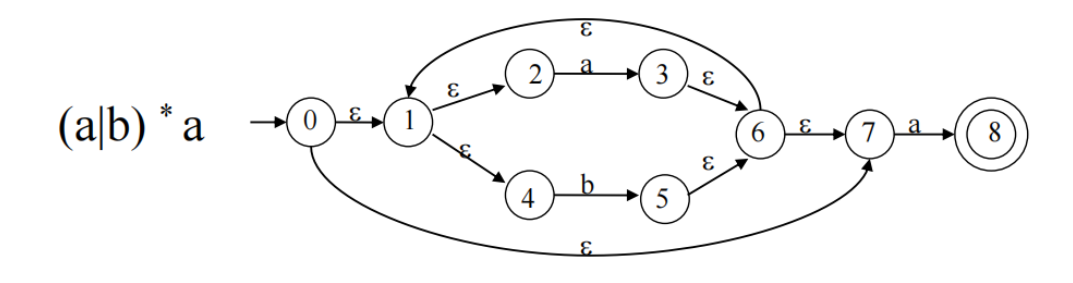
Tip :虽然 0 和 7 结点貌似可以分别由 1 和 6 代替,但仔细观察就可以发现如果替换将与原来的意思不同,替换之后由 1 直接到 6,6 仍然可以回到 1,而现在由 0 到 7 则不能再回到 0,也即失去 反悔 的机会。
2.11 题
题目 :可以通过正规式的最简 DFA 同构来证明正规式等价。证明下列正规式等价
解析 :
- 注意,PDF 的 2.8 题仅供参考,重点是理解思想,做法不一,以自己老师说的为准。
先画出 NFA,由 NFA 推导 ε-closure,然后得到 DFA,最后化简得到最简 DFA。
ε-closure(δ(A, a)) :表示从 A 集合中任何一个点出发,在输入 a 的前提下 可以走到的点的集合 ,例如点 2 在输入 a (隐含 ε)的前提下,可以推导出的集合为 {4, 6, 7, 1, 2, 3} 。注意通过 ∈ 转移到的点也视为符合条件。
对于最简 DFA,可以视为划分为包含 f 的状态所构成的集合和不包含 f 的状态所构成的集合。具体可看:最简DFA 7:20
对于给定的 DFA,如果状态集合中的某个状态无法通过任何输入字符转移到其他状态集合中的状态,那么这个状态就是不可细分的,也就不需要进一步划分。状态集合 F 中的每个状态都只能在集合 F 内部相互转移,没有办法将其进一步划分为不可细分的子集。因此,F 不需要进一步划分。
2.13 题
题目 :构造表示 0,1 个数都是偶数的01字符串的 DFA
解析 :
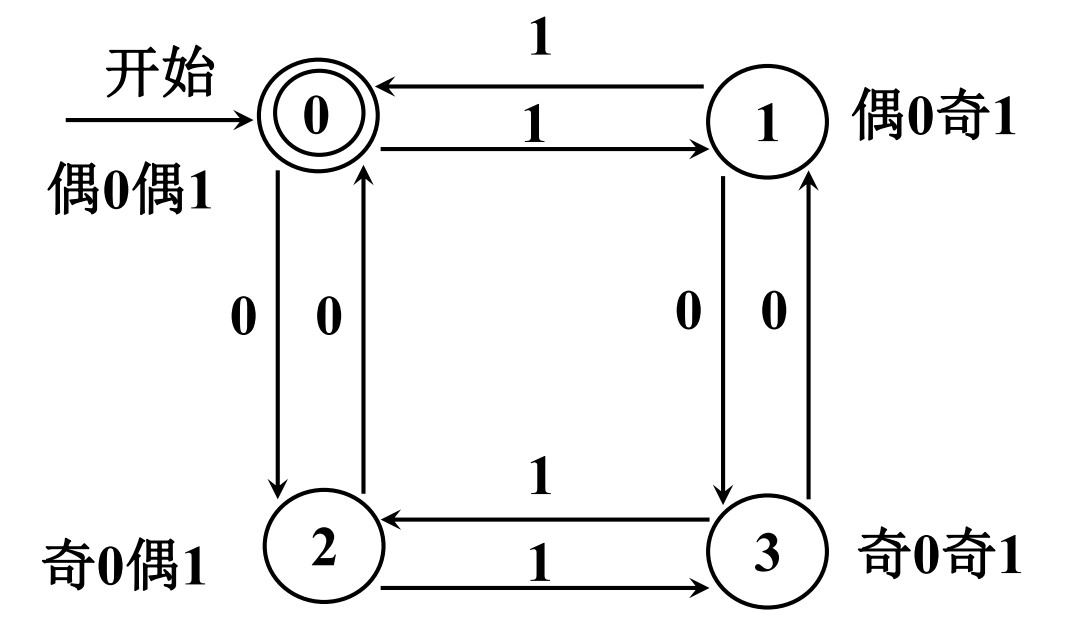
2.14 题
题目 :构造 DFA,识别 {0,1} 上能被 5 整除的二进制数
解析 :
注意 DFA 和 NFA 的最大区别:
- DFA 从每个状态出发,对于给定的输入字符,只能到达一个特定的下一个状态。
- NFA 在给定输入字符和当前状态的情况下,可以有多个可能的下一个状态。例如 2.7 题中从 1 号结点出发,给定
ε可以走到 2 和 4 号结点。
第三章
前缀知识
分析树是用于表示通过应用文法规则推导得到的句子结构的一种树形结构。
最左推导是一种推导句子的方式,它总是选择从左边开始的非终结符进行推导。在每一步推导中,最左推导总是选择替换产生式右侧的最左的非终结符。这种推导方式保证了在生成的过程中,每个非终结符都被展开为其最左的可能形式。
文法产生的语言是由该文法所能生成的所有句子组成的集合。
文法中的一条规则通常被称为产生式(Production Rule)或者产生式规则(Production Rule)。
文法二义性(Grammar Ambiguity)指的是一个文法规则可以推导出多个不同的句子或者一个句子可以有多个不同的推导方式。
3.1 题
题目 :考虑文法 S -> (L)|a , L -> L,S|S
(a) 建立句子(a,(a,a))和(a,((a,a),(a,a)))的分析树
(b) 为(a)的两个句子构造最左推导
© 为(a)的两个句子构造最右推导
(d) 这个文法产生的语言是什么
解析 :
建立分析树就是从上往下画图,以 S 为根,叶结点为终结符。注意单个产生式对应的子树。比如该题如果想要画出 (a, a) 就需要以 S 开头。
最左推导就是对照分析树,按照从左向右的方式,将非终结符替换为终结符。最右推导反之。
描述的语言对着文法说。
3.2 题
题目 :考虑文法 S -> aSbS|bSaS|ε
(a) 为句子 abab 构造两个不同的最左推导,以说明此文法二义
(b) 为 abab 构造对应的最右推导
© 为 abab 构造对应的分析树
(d) 这个文法产生的语言是什么
解析 :
用文法中不同的产生式规则替换非终结符 S。
另外三问参考 3.1 题。
3.3 题
题目 :下面的二义文法描述命题演算公式的语法,为它写一个等价的非二义文法 S -> S and S | S or S | not S | p | q | (S)
解析 :
为什么前两条有 |T 和 |F ?避免无限递归,比如如果写成 E -> E or T ,则 A and B and C 将被解析为 S -> S and S -> S and S and S 。
为什么是 E -> E or F ,替换为 E or E 可以吗?不可以,后者会导致二义性,因为它允许把一个表达式分解为两个相同的子表达式,例如,在解析表达式 A or B or C 时,我们可以通过 E -> E or E 产生式推导出 A or (B or C) 或 (A or B) or C,这就产生了二义性。 or 运算符是左结合的。
为什么括号里是 E ,将 (E) 替换为 (F) 可以吗?括号可以用于改变运算符的优先级和确定子表达式的计算顺序。使用 (E) ,可以递归地扩展为其他表达式。
3.8 题
题目 :(a)、消除3.1的左递归
(b)、在(a)的基础上构造LL(1)分析表
解析 :
- 直接左递归公式:
S->Sa|b可通过S->bS'和S'->aS'|ε得到。
分析表步骤:
-
先求 FIRST 集和 FOLLOW 集。
FIRST 集:所有候选式的串首终结符。
FOLLOW 集:针对非终结符,找出其后可能跟随的所有终结符。FOLLOW 集比较难以理解,下面简单说一下求法:
- 将
$加入到 识别符号 (也即 S)的 FOLLOW 集中。 - 若存在
U->xWY,则将FIRST(Y) - {ε}加入到 W 的 FOLLOW 集合中。 - 若存在
U->xW或U->xWY,后者需要 Y 可以推导出 ε,则将 U 的 FOLLOW 集合加入到 W 的 FOLLOW 集合中。 - 以上两点的 x 都可以为任意值。
- 将
-
LL(1) 分析表:
- 当非终结符 A 遇到其 FIRST 集中的终结符时填入相应候选式
- 当非终结符 A 的 FIRST 集中含有 ε 元素时,遇到其 FOLLOW 集中的终结符时填入
A->ε。
总结 来讲,找 W 的 FOLLOW 时,就看右部哪里出现了 W:
- 如果 W 后面直接跟着 终结符 ,就将终结符加入 W 的 FOLLOW 集;
- 如果 W 后面跟着 非终结符 Y,将如果 Y 的 FIRST 集减去 ε (因为此时需要 Y 不为 ε)后加入 W 的 FOLLOW 集合;
- 如果 W 后面没有任何东西,或者 W 后跟的 非终结符 可以推导出 ε,则将左部的 FOLLOW 集合加入 W 的 FOLLOW 集合中。
3.10 题
参考 3.8 题
3.15 题
题目 :(a) 用3.1的文法构造(a,(a,a))的最右推导,说出每个右句型的句柄
(b) 给出对应(a)的最右推导的移进-归约分析器的步骤
© 对照(b)的移进-归约,给出自下而上构造分析树的步骤。
解析 :
最右推导参考 3.1 题。
- 需要注意,求每个句型的句柄时最好对照分析树来看。
- 实际上就是将给定的序列,每次单个符号依次进栈,当栈顶出现某个 产生式 的 候选式 时,进行替换。
- 记得以
$开头。
构造分析树比移进-规约的步骤画图就可以了,不要忘记最后的 $ 符号。
3.16 题
题目 :给出接收文法 S -> ( L ) | a 、 L -> L , S | S 的 LR(0) 活前缀的 DFA
解析 :
LR(0) 活前缀 DFA 步骤:
- 首先用 S‘ 指向 S,构造一个产生式。
- 将每个产生式的候选项分成单独的产生式,并为所有产生式标号。
- 从
S'->S开始,将·加在产生式右部的开头,如果·后面是非终结符,则重复此步骤(例如,S 是非终结符,所以继续将以 S 开头的产生写在下面,并在右部开头加上·),记为状态 I0 。 - 从 I0 开始,每个状态按其内部产生式的个数,引出相应个数的状态。每个新的状态是以前一个状态的某个产生式的
·后移得到。
第四章
前缀知识
以下仅用通俗语言描述,只需要有个印象,否则直接做题短时间内很难接受陌生的知识。
综合属性:自下往上传
继承属性:兄弟或自上往下传
注释分析树:可视为给分析树添加注释。
语法制导定义:可视为解释产生式的动作。
翻译方案:复杂化的语法制导定义
4.1 题
题目 :根据表 4.1 的语法制导定义,为输入表达式 5*(4*3+2) 构造注释分析树。

解析 :
注释分析树:
- 先 从上往下 根据产生式 画出分析树。
- 再 从下往上 根据语义规则 补全注释。
4.3 题
题目 :为文法 S → (L)|a 、L → L,S|S
( a ) 写一个语法制导定义,它输出括号的对数。
( b ) 写一个语法制导定义,它输出括号的最大深度。
解析 :
将文法的每个候选式拆开,并以 S'->Sn 输出结果。在文法制导定义的每条后面写具体计算。
如果拆候选式时,右部出现了左部的符号,例如 S ->AS ,那么要将右部的 S 改为 S1 用以和左部区分。
用 递归的回溯过程 视角 从下往上 看分析树,就会发现很好理解。虽然这道题看起来和 4.1 不同,但其实很相似,画分析树的过程就是向下递归的过程,由非终结符终止递归;补全注释的过程就是向上递归回溯的过程。
4.10 题
题目 :文法如下: S → (L)|a 、L → L,S|S
( a )写一个翻译方案,它输出每个 a 的嵌套深度。例如,对于句子 ( a ,( a , a ) ),输出的结果是 1 2 2。
( b )写一个翻译方案,它打印出每个 a 在句子中是第几个字符。例如,当句子是 ( a , ( a , ( a , a ) , ( a ) ) ) 时,打印的结果是 2 5 8 10 14。
解析 :
明确了什么是翻译模式后,这道题以 自上往下看 的视角就很容易理解了。依然是拆解文法的候选式,注意由 {} 括起来的语义动作在新产生式右部的位置就可以了。
简单一句话概括就是:所谓翻译模式,就是在语法制导定义中 明确计算顺序 。在某个 字符前计算该字符的值(例如 S.depth = 0 或 L.depth = S.depth + 1 ),在该字 符后使用该字符的值(例如 print ( S.depth))。
个人推荐不必细究其明确的学术定义,如果只是希望会做题,那么不需要知道为什么。
关于第二问:
-
第二问的重点在于理解什么时候需要加 1,例如
S->(L),S 推导出的(L)前多了字符(,所以需要加 1。 -
关于 in 和 out。在右部 每个非终结符之前计算其自身 in (继承)属性的值,在 式子最后计算产生式左部 的 out (综合)属性值。翻译模式重点在于明确计算顺序。
out 表示句子中该文法符号推出的字符序列的最后一个字符在句子中是第几个字符。
个人感觉将 out 含义描述中的 字符 改为 终结符 更容易理解。
-
是否必须要用两个属性(
in和out)?首先答案肯定是TRUE,因为答案就这样写的,如果能用一个属性没理由写复杂。然后就要想为什么,个人理解是因为:- 综合属性 是向上综和的,所以综合属性只能计算当前子树的值(也即从叶子结点回溯到子树根节点得到的值)。
- 继承属性 是向下继承的,所以通过继承属性可以得到之前子树的值。
- 而我们在计算每个字符的位置时,不仅需要当前子树的值,还需要之前子树的值。大概这么个意思。
4.13 题
题目 :下面是构造语法树的一个 S 属性定义。将这里的语义规则翻译成 LR 翻译器的栈操作代码段。

解析 :
个人理解:
- 将产生式左部全部用
var[ntop]替换。 - 将产生式右部从左向右依次加入栈,然后按照每个符号距离栈顶的位置替换其在语义规则中的位置。例如
E->E1+T,入栈顺序依次是E1、+、T,其中T在栈顶,E1位置是栈顶向下 2 个位置,所以E1用var[ntop-2]替换。 - 终结符和函数名照抄。
- 如果产生式右部只有一个非终结符且位于栈顶,则可以省略。
以下为例题补充 :
4.4 题

解析 :
重点在于看出什么时候打印出错信息:当 ab 的数量和 c 的数量不同时表示出错。还是以 从下往上 看的视角,如果 递归回溯 到起始节点,发现 ab 和 c 的信息不同,则表示出错。
4.12 题

解析 :这题扫了一眼就困了,下午再看 : )
注意点
第二章
NFA 和 DFA 的终结状态用两个圈表示。第一个状态前的输入是 start 。
DFA 包含 NFA 终结状态的集也要用两个圈表示。
第三章
描述文法产生的语言时,依然找数量和位置关系。
消除左递归: S->Sa|b 的左递归可通过 S->bS' 和 S'->aS'|ε 消除。
求 FOLLOW 集时,要在开始状态中加入 $ ,如果后续某个状态的 FOLLOW 集包含开始状态的 FOLLOW 集,则也应该将 $ 一并加入。
画 LL(1) 分析表时,如果 FIRST 集中包含 ε ,则再去看 FOLLOW 集。并且 LL(1) 第一行要在最后补上 $ 。
画移进 - 规约表时,栈的第一个字符和输入的最后一个字符都是 $ 。当栈中只剩开始状态时,动作为接受。
第四章
语法制导定义和翻译模式:
- 要有
S'->S。 - 明确看的顺序:从上往下看,就计算右部非终结符(的继承属性);从下往上看,计算左部非终结符(的综合属性)。
- 两个属性的题都计算,在右部非终结符前计算(右部非终结符的)继承属性,在式子的最后计算(左部非终结符的)综合属性。



