题目链接:KMP字符串
题意:
题意很简单,给定一个模式串S和模板串P,问P在S中出现的所有位置。第一反应,似乎可以暴力 <-- 这种思想虽然不能说好,但是往往有奇效hhh。
思路:
看完y总视频总觉得要写一写总结一下,有种不吐不快的感觉hhh
- KMP的思想其实很简单,但是很神奇很奇妙,重点就是next数组的构造和使用。
- 我们先想想暴力怎么做,然后考虑怎么优化。朴素算法我们当然是从0开始遍历模式串的每个字符,从它开始一一对应模板串的每个字符。
- 那么问题就是:如何优化?
- 显然我们很难去优化第一重循环(也即模式串的遍历),那么我们可以从第二重循环(对模板串的遍历)下手。思考这样一个问题,当我们指向模式串S第i个字符的指针向后移动了一位,我们的模板串P需要从头开始遍历吗?
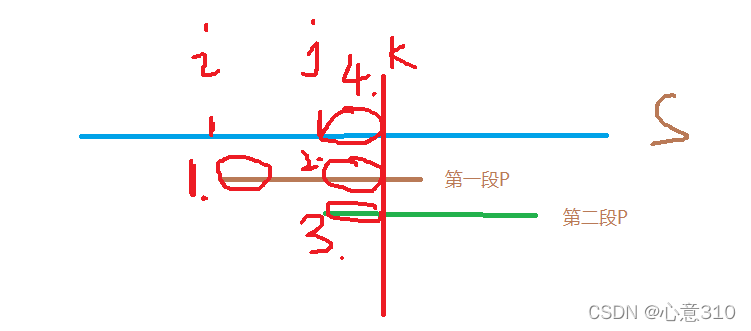
- 我们可以看这张图,假设第一段P串开头走到S[i]位置,然后在S[k]位置与P无法匹配,那么我们显然要让P往后走,假设当第二段P串开头位置走到S[j]位置可以匹配,那么我们就会发现一个有趣的性质,第二段P[j,k]和S[j,k]相等,第一段P[j,k]也是和S[j,k]相等的,所以这两段P其实是相等的(第一段就是上面的P串,第二段就是下面的P串)。 而这里画圈的3实际上就是画圈的1平移过来的。
- 于是我们发现如果S和P串在某个位置不匹配,那么P要向后走到某个位置,这个位置满足P从无法匹配处的后缀与P的前缀相等。
- 那么我们就可以构造一个数组取名为next,next[i]中存的是以i为终点的后缀与前缀最大的匹配长度,同时长度要严格小于i。
KMP实际上就是模板串P要向后移动多少这么回事 - 而next数组的构造同样可以用到KMP的思想。我们来看具体到代码如何实现。
补充:
注意体会next数组:
- 首先next[i]是要小于i的。
- 其次我们说如果s[i]与p[j+1]匹配不成功,就使j后退到next[j]的位置,这实际上是说我们首先将p字符串开头位置与s[i]对齐,然后整体向右走next[j]长度,注意体会这里的两个描述,他们的含义其实是相同的。
- 在构造next数组时,我们可以假设构造到next[i]的位置,那么前面的next[j-1]已经构造好了,我们可以直接去看p[j+1]和p[i]是否相等,如果相等我们就令p[i]=j+1,否则我们就将j退回到next[i-1]的位置,因为此时一定有一个最长的后缀与前缀相等。
- 为什么是看p[j+1]和p[i]?因为我们假设next[i-1]的长度是j,那么p[1,j]和p[i-j,i-1]一定是匹配的,我们可以直接看当前点p[i]与p[j+1]是否匹配即可。
- 这个KMP的模板时间复杂度是O(n)
代码:
#include<iostream>
#include<cstring>
using namespace std;
const int N=1e5+10,M=1e6+10;
int n,m;
char s[M],p[N];
//next[i]表示以i为终点的后缀与前缀最大的匹配长度,同时长度要小于i
int ne[N];
int main()
{
//kmp字符串从1开始
cin>>n>>p+1>>m>>s+1;
//构造next[i]数组,因为next[i]<i,所以next[1]=0;
for(int i=2,j=0;i<=n;++i)
{
while(j>0&&p[i]!=p[j+1])j=ne[j];
if(p[i]==p[j+1])j++;
ne[i]=j;
}
//kmp匹配过程
for(int i=1,j=0;i<=m;++i)
{
//如果此时j没有推到模板串开头,并且s[i]与p[j+1]不匹配,那么j推到next[j]
while(j>0&&s[i]!=p[j+1])j=ne[j];
//如果匹配成功,i和j一起向后移动一位
if(s[i]==p[j+1])j++;
//匹配成功
if(j==n)
{
//在输入字符串时是从1开始的,所以要减1,i-n+1再-1也就是i-n
printf("%d ",i-n);
j=ne[j];
}
}
return 0;
}


